Π Calendar
Bridging the Scales
The Pi calendar was created in an effort to validate early concepts of the primer. These arguments are a baseline for the structural integrity of Prime Mechanics.
*In Prime Mechanics, orders of magnitude (such as scales of Base-10 within the range of the Irrational and Natural number fields) are reduced to a single ternary loop structure. This is because Pi is assigned the value [3Xx) – while Classical Mechanics may assign a decimal and fractional value to Pi, Prime Mechanics sees Pi as an expression of fractal geometry. This is explored in depth in additional works on PM.
The calendar was mapped on June 30, 2020, and is considered as such due to its ability to account for the following:
-The close approximation of Pi at 22/7
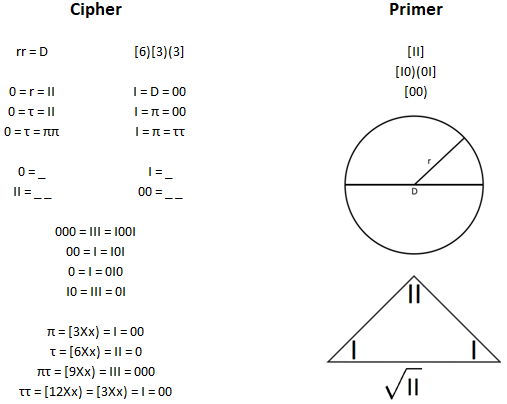
-The expressions of Pi as [3Xx) and Tau as [6Xx) where 00 == I and II == 0 (2Tau == Pi and 2Pi == Tau)
-A valid II(0)-dimensional mapping of the Inverse-Square Law
-An unfoldable geometry equivalent to the ‘frozen’ qubit expression [00)[I0)(0I][II]
-A multi-dimensional geometry stemming from Absolute Zero where 00 == I
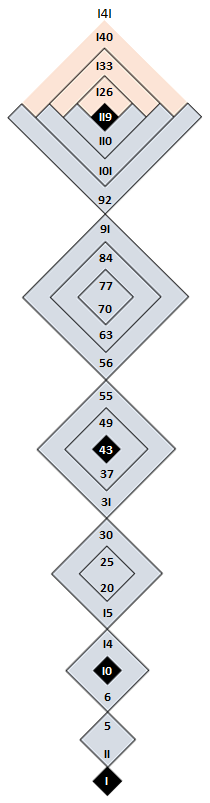
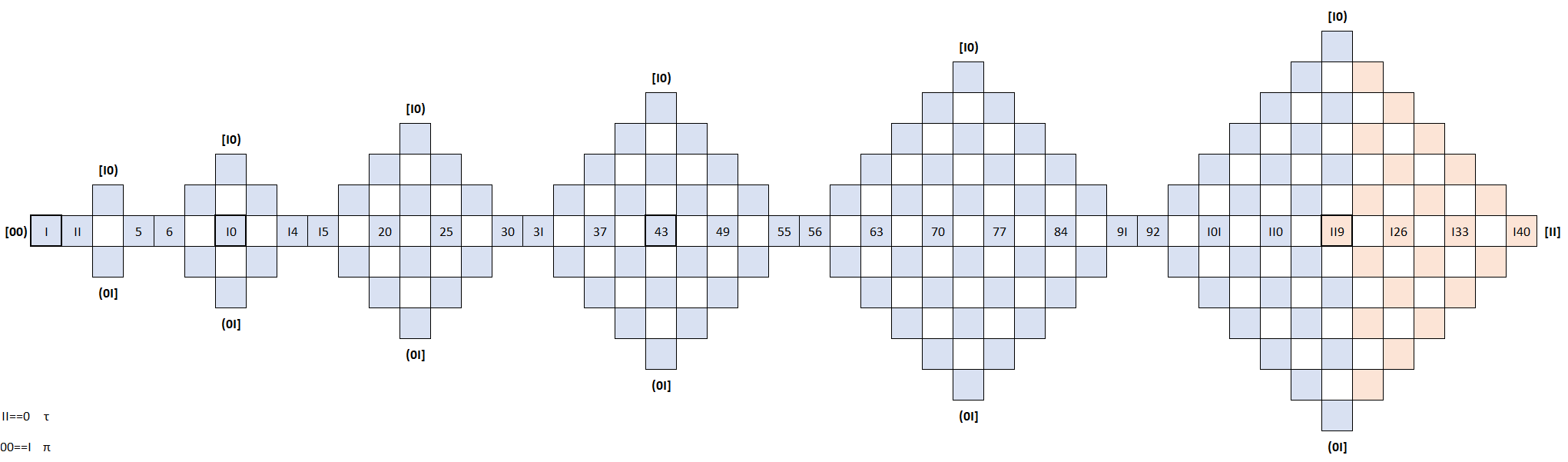
-A structure that fixes Element 119 at a horizontal threshold, or event horizon of observed elements*
It is useful to know here that the outer limit – Element 141 – the initial value of the 8th Inverse-Square iteration, is expressible as [141)[72)[36)[18)[9)[6)[3)(3] using Prime notation. This is explained in depth further below. Naming the elements is a wasted opportunity in the lens of Prime Mechanics because it detracts entirely from the mathematical structure (atomic number). It is also important to note that Prime notation does NOT rely on elements as units, they are simply one group of values that may be mapped using Prime notation.
*Because Time is not measured in the same units as Classical Mechanics (Base-60 for Seconds and Minutes, for example), those forms in Nature which are measurable and constant are considered valid. In the case of atomic numbers, iterations of protons may be expressed within the first quadrant of the four-quadrant (Cartesian) system of Classical Mechanics because they have a fixed positive (+) charge. All three components to the atomic structure (Protons, Neutrons, Electrons) as well as the underlying Standard Model are considered to be map-able through the model using Prime notation – it is at this point a matter of conversion.
For those that have read previous works (available here) it is shown that the calendar is expressible in any number of ways, however it operates solely within the first quadrant, rotated 45 degrees counter-clockwise. Understanding wave functions (Sin,Cos,Tan) along with the Exponential and Logarithmic functions is a secondary goal of the project – the priority as of August 2020 is to open PM to public scrutiny and development while continuing to build upon the language structure.
To further understand the open source nature of the project and why it actively counters incentivized competition (monetary, celebrity or other personal gains at the expense of communal growth), visitors are encouraged to learn about The Cathedral and the Bazaar, a software development concept shared by Eric S. Raymond in 1997.
The Pi calendar is given its name because it demonstrates the ternary functionality of Π as Absolute Zero, in which the underlying components are those elements that have been observed within the universe itself. Where II == 0 and 00 == I ( again, 2Pi == Tau and 2Tau == Pi), we are given the ability in Prime Mechanics to learn beyond the Time construct (limit) of Classical Mechanics (in CM, 2Tau == Pi is invalid – this root argument establishes a binary, or directional foundation – PM is non-directional). This will continue to be expanded upon over the ongoing development of the language.
Because Pi is Absolute Zero in PM (I == 00), fractals provide an alternate visualization of the expression. While the Mandelbrot set is only one type of fractal geometry (it is hypothesized at this point that Pi is represented within all expressions of fractal geometry), its 1-dimensional surface IS Pi in PM because 1-dimensional equates to ‘I’-dimensional (I == Pi is the essence of both the cipher and primer of the language). In the case of the Mandelbrot set (an eponymous term for an observable figure) the I-dimensional surface which may be zoomed into is the aspect of the set that is infinitely diverse yet consistently structured. This base is understood as a ternary structure in Prime Mechanics where Pi == [3Xx) (in CM, fractional and decimal expression of Pi require a Natural number of 3 as a permanent integer). Where 3.1415926… and 22/7 == 3 1/7 provide approximations, geometrically Pi is expressed as the ratio of Circumference to Diameter, with its partner Tau the ratio of Radius to Diameter. The value of Tau as [6Xx) is also understood more aesthetically through Prime notation.
Prime notation (I,0,III) allows us to map any Natural number to a looped expression. For example, when given any number, we may reduce it to its minimum expression. Where a number value of three spaces _ _ _ is greater than a value of two spaces _ _, PM bridges digital and non-digital numerology by stating that I == Pi (I bit, , I proton, I person, I cat, I quark, etc.). This allows for a reduction to one of three possible Prime values.
Some numbers can be two or even all three of the Prime values. For example, ten (10) in Classical Mechanics is equal to ten (10 == 10). In Prime Mechanics, however, we may state that I0 == I and I0 == III. Before expanding on the order of operation, let’s consider a handful of examples:
[12)[6)[3)(3]
[11)[7)[5)[4)[2)(0]
[10)[5)[4)[2)(1]
[9)[6)[3)(3]
[8)[4)[2)(0]
[7)[5)[4)[2)(1]
[6)[3)(3]
[5)[4)[2)(0]
[4)[2)(1]
[3)(3]
[2)(0]
[1)(1]
The linear expressions of the numeric values create a structure across their unfolding – this is the loop functionality of the language. [6)[3)(3] for example equates directly and always to Carbon, but also any other sets or groups correlating to the value six. This becomes more intuitive when one recalls in Prime Mechanics that Pi == [3Xx) and Tau == [6Xx), with 2Tau, or [12Xx), reducible to [3Xx).
[12)[6)[3)(3]
[11)[7)[5)[4)[2)(0]
[10)[5)[4)[2)(1]
[9)[6)[3)(3]
[8)[4)[2)(0]
[7)[5)[4)[2)(1]
[6)[3)(3]
[5)[4)[2)(0]
[4)[2)(1]
[3)(3]
[2)(0]
[1)(1]
IIIIIIIIIIII == 000000 == III == 000
IIIIIIIIIII == 0000000 == IIIII == 0000 == II == 0
IIIIIIIIII == 00000 == IIII == 00 == I
IIIIIIIII == 000000 == III == 000
IIIIIIII == 0000 == II == 0
IIIIIII == 00000 == IIII == 00 == I
IIIIII == 000 == III
IIIII == 0000 == II == 0
IIII == 00 == I
III == 000
II == 0
I == 00
12 == I0 == III == 000
11 == II == 0
10 == I0 == III == 000
*Single-digit numbers can only have one Prime value – numbers that have more than one Prime value (I,0,III) are most effectively mapped using their value that reinforces the ternary loop across any given set of values. Where 10 is equal to both I and III, I is true to the order of operation while also establishing 11 as 0.
In PM, the fewer characters used to represent a value, the more efficient it is. I is more efficient than 00, and 0 is more efficient than II. Since 0 contains I more than I (as II), only I and 0 are required to annotate a ternary loop.
The order of operation is simpler than it may seem – to begin, because any number in Prime Mechanics is Natural, we may consider any given number merely a grouping of individual units – they are together and yet distinct. The tally system is the most natural and intuitive way to express this.. Here is the critical next step – where an individual unit is equal to I, this unit can be converted to 00. This allows us to convert units using binary notation without losing any information, a form of lossless data compression. Where III == 000 is the last value in Prime notation (I,0,III), once we reach beyond III we revert back to I (4 is IIII –> 00 –> I).
For even values, we divide by two continuously until we reach an odd number or one of the Prime values.
For odd values, we add three then divide by two, repeating this for each odd value until we reach a Prime value.
We can use the above two operations for any Natural number, considering additional examples below:
[88)[44)[22)[11)[7)[5)[4)[2)(1]
[87)[45)[24)[12)[6)[3)(3]
[86)[43)[23)[13)[8)[4)[2)(0]
With an even number like 88, it is fairly simply to continue dividing by 2 until we reach an odd number. At 11, we simply add three then divide by two – this allows us to convert from I to 00. IIIIIIIIIII becomes IIIIIIIIIIIIII – we then convert these 14 units to seven zeros, 0000000. To get to 5 from 7, we add three, 0000000000 and again divide by two – IIIII. Writing out individual lines followed by individual zeroes is an inefficiency when we understand how the conversion works – we simply convert to binary using I == 00 and II == 0 in order to reduce each expression while retaining the initial unit value.
Ordering the above numeric structures into binary sets (tallies to zeroes to tallies etc.), we may establish a linear expression:
9 iterations,
7 iterations,
8 iterations,
Where I as 00 and 0 as II gives us:
(88) I – 0 – I – 0 – I – 0 – I – 0 – I
(87) I – 0 – I – 0 – I – 0 – I
(86) I – 0 – I – 0 – I – 0 – I – 0
*There is no distinction between the scales of universal phenomena in Prime Mechanics because Absolute Zero is valid as 00 == I, where 00 (2Tau) establishes a constructible plane in II(0)-dimensional space. The X-Y coordinates for Absolute Zero in Classical Mechanics may be considered (0,0) where 0 Kelvin equals -273.15 degrees Celsius (remembering that there can be no value less than zero in Thermodynamics, as this zero is unattainable by the laws themselves).
While a review of Prime notation may help prior to measuring the structure below, the linear order of operation for ‘element’ 141 is provided here:
[141)[72)[36)[18)[9)[6)[3)(3]
We may recall that this gives us 8 iterations in binary:
I – 0 – I – 0 – I – 0 – I – 0
In order to map the expression II(0)-dimensionally, we must double each iteration stemming from the Prime value. There is a precise name for this in Classical Mechanics – the Cantor set (eponymous label for a ternary loop structure of non, zero, one). While Cantor logic has importance within Classical Mechanics, it does not have a name in Prime Mechanics because the ternary structure exists independently of an eponymous label. To double a given expression, we may first state:
141 – 8(0)
72 – 7(I)
36 – 6(III)
18 – 5(0)
9 – 4(I)
6 – 3(III)
3 – 2(0)
3 – 1(I)
In this conversion the base value is always I because we are beginning from Absolute Zero (00 == I). Unfolding with a fixed middle-third across each new value, we arrive at the following:
1411411411411411411417272727272723636363636181818189996633366999181818183636363636727272727272141141141141141141141
While this communicates the sequencing in one way, we may expand it II-dimensionally by understanding the primer:
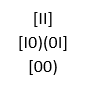



The ternary loop I,0,III establishes a structure that is not bound by the limits of Classical Mechanics. Each element has at least one Prime value -the lowest numeric value to have two Prime values is 10, frequently demonstrated as being equal to I and III in Prime notation.
By relying on a uni-directional (forward-diagonal) expression from Absolute Zero (00 == I, 0 == II, III == 000 per the cipher), we may assign color values that correspond to temperature shift while providing the underlying wave mechanics of an unfoldable ternary structure over Time (where Time is I(Pi)-dimensional).



A free copy of the above calendar expansion along with the conversion table below are available here.