Curiosities
UPDATED Dec. 17, 2022
Base Systems
UPDATED Jun. 22, 2022 – Base systems allow us to formulate constructs in multiple dimensions by utilizing different radices. Most of the modern world (2022) relies on Base-10 (decimal, which has a radix of 0-9), but Base-60 is also used for measuring time, while Base-2 (binary) and Base-16 (hexadecimal) are common in computing. Any number of base systems have been in use around the world at different times.
The conversion from Prime notation to the Base-10 radix was an early discovery: I = 1, 4, 7; 0 = 2, 5, 8; III = 3, 6, 9. Base-10 provides a method for evaluating simple and complex systems , and so it is currently the main base system being used. Ultimately, however, the very necessity for different base systems is seen as a limitation of the Real Number system.
The idea of bits vs non-bits (also, digital vs non-digital) is given a radically different framework when using PM vs conventional mathematics. For example, Base-2 (I and 0) relies on Real Numbers – this in turn establishes a preconceived notion as to their form and function, and theorists may debate the properties of bits (or any fundamental forms of matter) as energy existing at scales such as the Planck length. I and 0 are always equivalent to Pi and 2Pi(Tau) in PM, and so the framework that branches from this foundation will undoubtedly provide a different means for understanding the duality inherent to binary concepts within Classical Mechanics.
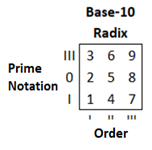
It’s important to note that one of underlying hypotheses of Prime Mechanics prior to its development was that ultimately, there is no need to extend beyond a single base system’s radix in order to measure any type of phenomena. For example, to extend beyond 9 in a Base-10 system would be considered a redundancy. The story about Asimov on the Fundamentals page adds some scope to this – when we consider the use of orders of magnitude in understanding both micro and macroscopic scales (also relying on Base-10), we’re merely adding complexity to a closed loop (radix) through repetition and expansion (10^-10, 10^-1, 10^0, 10^1, 10^10…). This concept of redundancy beyond the initial radix can be further reduced to Base-2 (binary) and even Base-1 (unary). In CM these radices do not serve as the actual limits of a given application – the concept of entropy is (within the scope of this work) considered a byproduct of this perspective, one that requires added complexity in order to solve fundamental problems of physics.
Prime Numbers
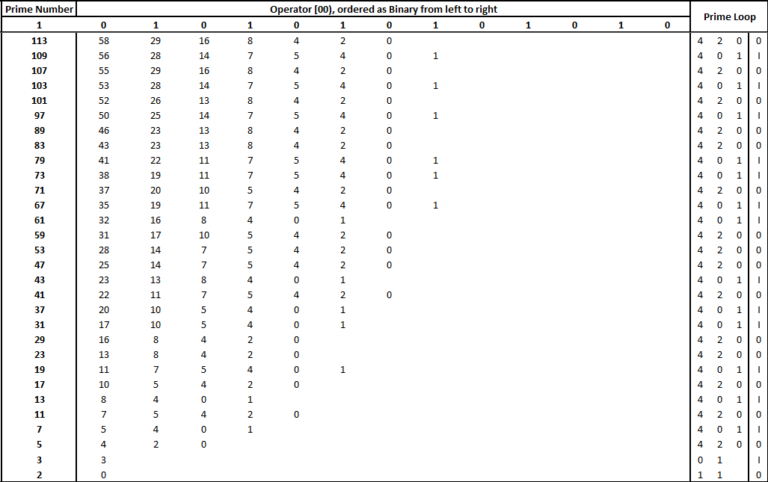
UPDATED Jun. 21, 2022 – Primes, like all Natural Numbers, are simply considered iterations of Pi in PM. In the table below we can see that, as opposed to other number series, Prime Numbers do not reduce to [6)[3)(3], the closed loop of the three main sequences in PM. Further work may consider the distribution of the remaining two sequences to see if there is a method for predicting or determining the distribution of primes.
Prime Mechanics derives its name from the use of Pi as the standard unit value as well as the main operator of the notation. For example, when considering the III Laws of PM (I == 00, II == 0, III == 000), Pi as an operator at Absolute Zero is expressed as [00). There is no correlation in this regard between the name ‘Prime Mechanics’ and prime numbers.
When considering primes, it is important to recognize that 7 is the
highest prime number within the Base-10 radix. While prime numbers
themselves may be understood differently using PM, 7 as the highest
prime within this limit of 0-9 makes it a simple but fascinating value.
Root 2: 1.4142135623730950
Pi: 3.1415926535897932
22/7: 3.1428571428571429
1/7: 0.1428571428571428
Fibonacci Sequence
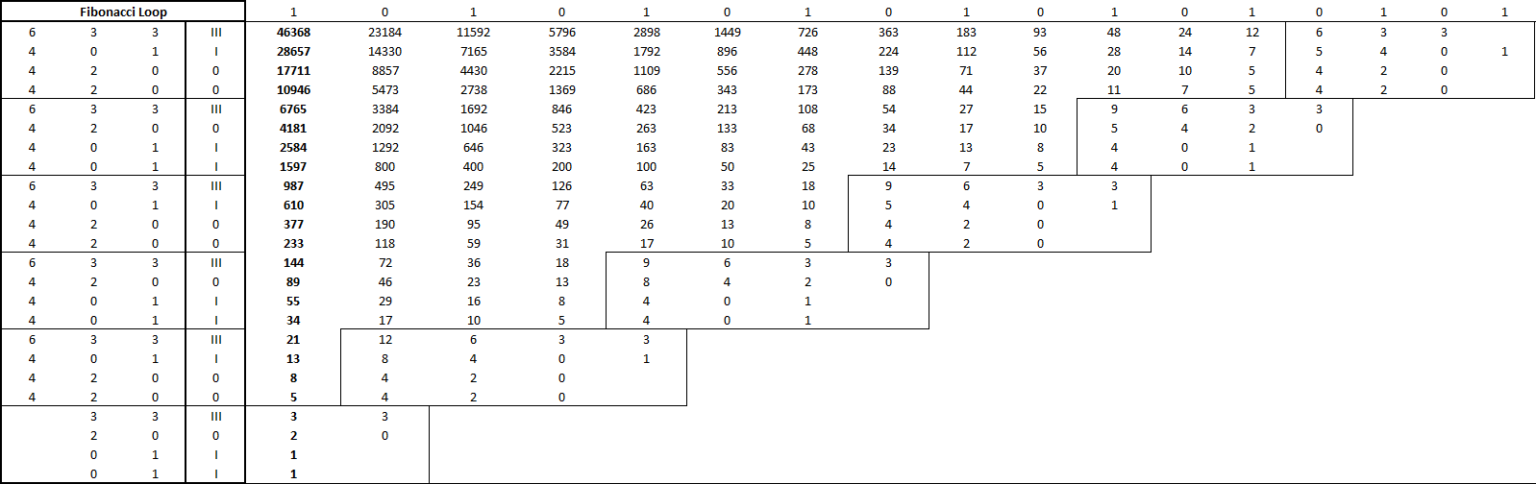
UPDATED Apr. 21, 2022 – This sequence is one of the best early examples of the capability of PM to derive simple sequences from more complex patterns. When converting Fibonacci numbers using the III Laws of PM, we arrive at an elegant loop: I I 0 III 0 0 I III. The 0’s in this case may also be considered II’s, but the 0’s are A) more efficient expressions as single-digit characters (_ vs _ _ , or 0 vs II) and B) they allow us to distinguish their step in the binary conversion process (see the very top row in the image below). This conversion process follows the ODD and EVEN rules applied by the III Laws.
Collatz Conjecture
UPDATED Dec. 17, 2022 – Saw a video by Veritasium on YouTube and couldn’t help myself : ) The Collatz Conjecture relates to the first of the three looped sequences in PM, [4)[2)(1] (2 and 0 being interchangeable per the second law of Prime Mechanics and synonymous with 2Pi equals Tau in traditional mathematics -known here as Classical Mechanics- where C/d = 3.X and C/r = 6.X). In PM, these ratios are also expressible as [3Xx) and [6Xx). Those who are familiar with PM already know the second and third looped sequences, bottom-to-top:
[6)[3)(3]
[4)[2)(0]*
[4)[2)(1]
The third sequence may look aesthetically familiar given II = 0, Pi = 3.X AND Tau = 6.X:
[6)[3)(3]
——————————————–
*[4)[2)(0] is actually [4)[2)(1] when following EVEN = N/2, however I and 0 are also used to define the iterations of the conversion process itself (defined by the III Laws of PM). As a random example, the value 23 is a 6-step conversion: I-0-I-0-I-0, which correlates to: [23)[13)[8)[4)[2)(1] which is then written as [23)[13)[8)[4)[2)(0] in order to distinguish the final iteration of 23 from its predecessor, [22)[11)[7)[5)[4)[2)(1], or I-0-I-0-I-0-I.
——————————————–
The problem of the Collatz conjecture per the video is that it’s missing a closed loop needed in order to validate it. The method used in the conjecture is as follows:
ODD: (3X+1)/2
EVEN: X/2
The pre-established method used in Prime Mechanics is:
ODD: (3+X)/2
EVEN: X/2
Remembering that I is assigned the value Pi, Pi(C/d) equals 3.X AND Tau(r/d) equals 6.X. The closed loop is quite literal: [6)[3)(3]. Reference was made when providing this tutorial in the comments section of the video that the values of the Fibonacci sequence, when broken down using the method of PM, provide an 8-loop: I,I,0,III,0,0,I,III
I also noted that none of the prime numbers converted thus far have resulted in [6)[3)(3] – only [4)[2)(1] and [4)[2)(0]. What wasn’t stated in the comments was that the closed loop problem of the conjecture took less time to solve than getting through the first half of the video – having recognized the above methodology of PM.
Fractals
Stay tuned…
Banach-Tarski Paradox
Stay tuned…
Brachistochrone Curve
Stay tuned…
Transcendentals
Stay tuned…
Euler's Identity
Stay tuned…