Fundamentals
UPDATED Apr. 25, 2022 – Stay tuned for the expansion of this page.
1, 0 and i
UPDATED Apr 25 – There’s a famous story about Asimov that relates to Imaginary Numbers and One. Asimov and a professor are debating the value of a piece of chalk that the professor breaks into two pieces. The professor states that the piece Asimov holds in his hand is half a piece of chalk, while Asimov declares that it is still one piece of chalk. This philosophical short story recognizes a fundamental division within the Real Number system.
In PM, Pi is synonymous with One and 2Pi (Tau) is synonymous with Zero – there are no imaginary numbers and in fact there are no standard units beyond Pi. In the case of Asimov’s chalk story, the intact chalk would be considered a ‘Pi’ unit of chalk, and each broken piece of chalk would also be considered a Pi unit. Scalability becomes a radically different concept when the current paradigm relies on orders of magnitude via Base-10 for things such as the physical constants (consider standard unit measurements and the micro/macro scales).
Demonstrating precisely how PM integrates imaginary numbers is a key step in converting Classical Mechanics (CM) to the language’s notation.
Geometry
UPDATED Apr 25 – This section will explore Prime notation as it relates to some of the most basic representations of number groups from CM. Early work will focus on polygons, especially the 45-45-90 triangle.
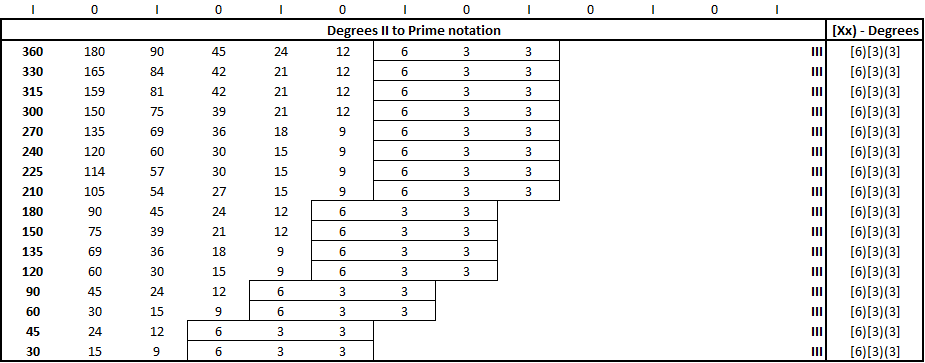
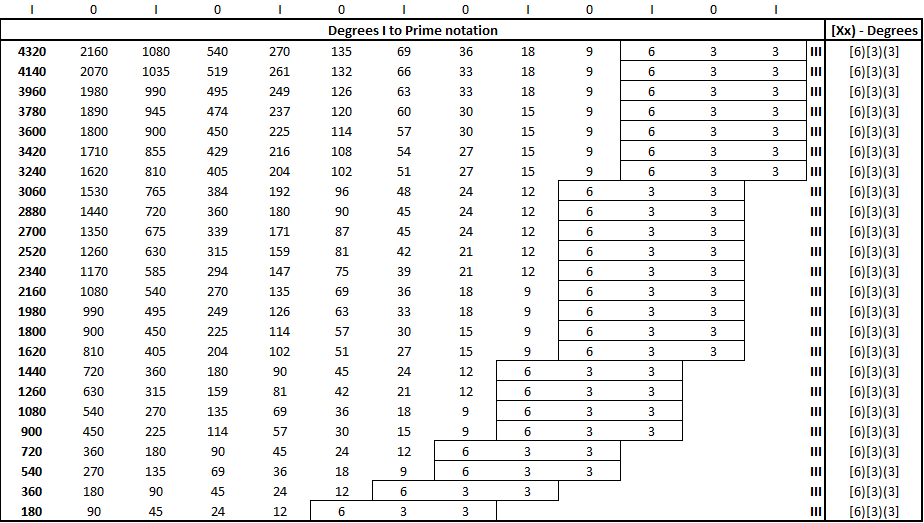
In the first image above, we can see that from 0-360 degrees, each degree is reducible to the closed loop [6)[3)(3], the third of the looped sequences in PM. This is an elegant display of the language’s notation, recalling that in CM A) Pi = C/d B) Tau = C/r and C) 2r = d. The second image expands upon the first 360 degrees, and we can see that the closed loop of [6)[3)(3] remains.
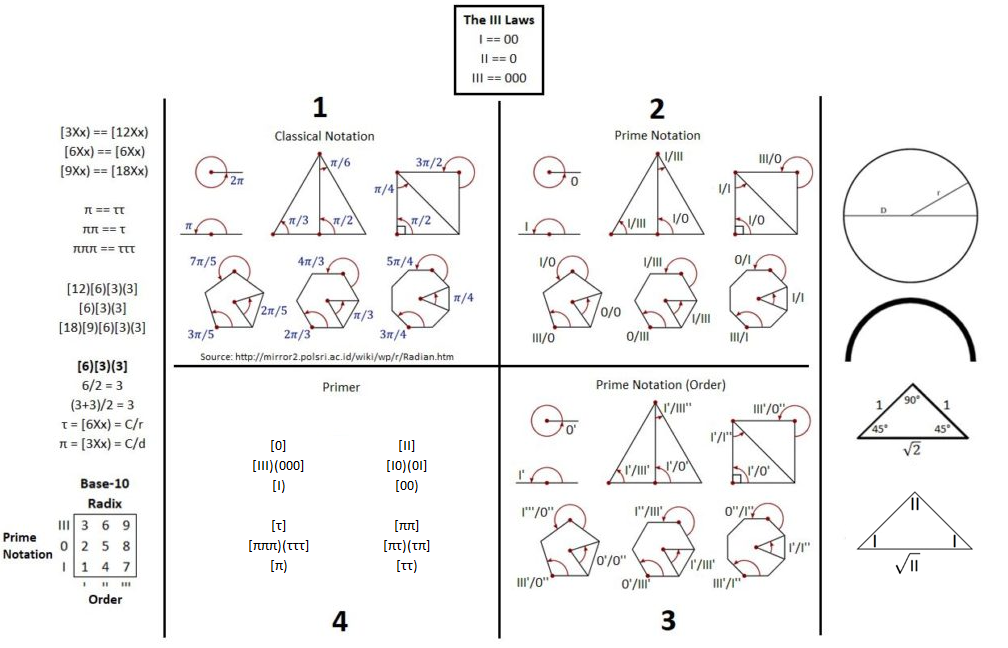
Algebra
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Probability and Statistics
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Calculus
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.